Machine learning Algorithm - Logistic Regression

What is logistic regression

Logistic regression is a supervised machine learning algorithm mainly used for classification tasks. The goal is to predict the probability that an instance belongs to a given class or not. It is a kind of statistical algorithm, which analyzes the relationship between a set of independent variables and the dependent binary variables.

It is worth noting that although “logistic regression” is the name given, it is not regression, essentially. Regression problem is a knd of problem which label is a continuous number, while classification problem is a knd of problem which label is a “category”. In fact, logistic regression is a classification algorithm.

Two-class classification

In the last article, we introduced the concept and calculation of linear regression. Similarly, let’s define cost function as:

where

We use Sigmoid function or logistic function g(z) to map real numbers into probabilities in range [0, 1] and represent how certain the data belongs to a category. Sigmoid function is shown as below.

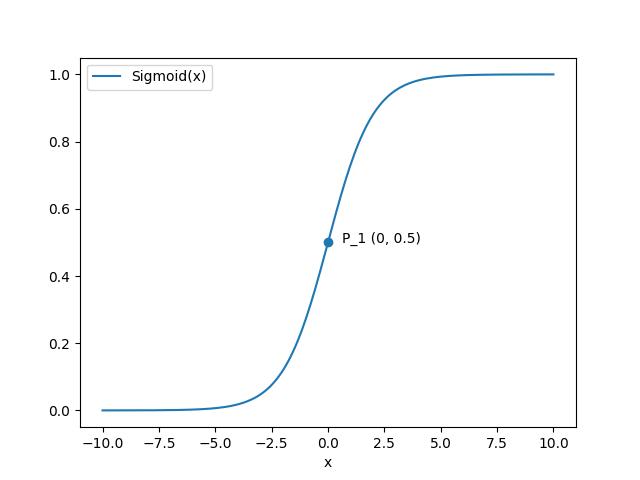
In most cases, we take P_1 as threshold of probability. In other words, if the output of hypothesis function is greater than 0.5, we predict the data belongs to label 1. On the contrary, if the output is less than 0.5, we predict the data belongs to label 0.

Binary cross-entrophy cost function

Entrophy

First of all, we need to know what entropy is. The physical meaning of entropy is a measure of the degree of chaos in a system. Later, Shannon introduced the concept of entropy into information theory and proposed the so-called “information entropy” concept. From the perspective of probability theory, it means that the greater the uncertainty of an event, the greater the information entropy. The entropy mentioned below refers to “information entropy”.

The calculation formula of information entropy is as follows, where p(x_i) is the probability that event P occurs in the i-th category.

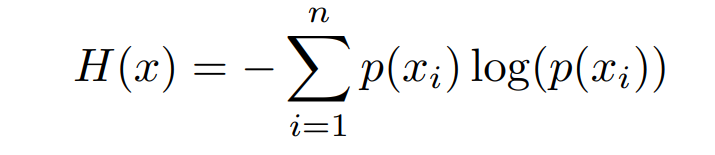
Kullback-Leibler divergence and cross entrophy

Before talking about cross entropy, we should also mention Kullback-Leibler divergence (KL divergence). KL divergence can be used to measure the similarity of two distributions. For example, in machine learning, we can use KL divergence to measure the difference between the true distribution and the predicted distribution of a set of sample. The formula for KL divergence is as follows:

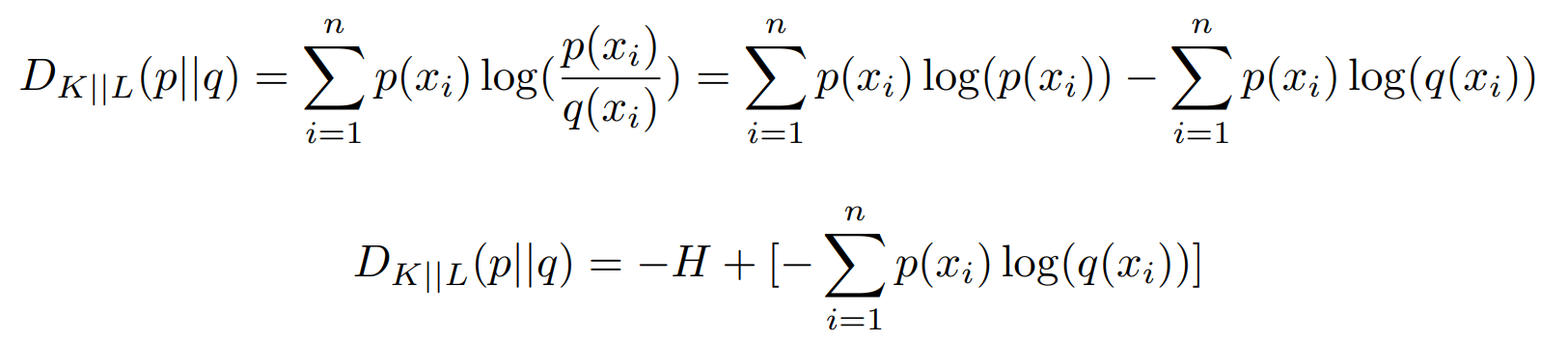
For a specific data set, the true distribution of the sample is known, so the entropy H of the true distribution is fixed, and the value of KL divergence is only related to the later part, which we call as “cross entropy”. Cross entrophy is defined as follows:

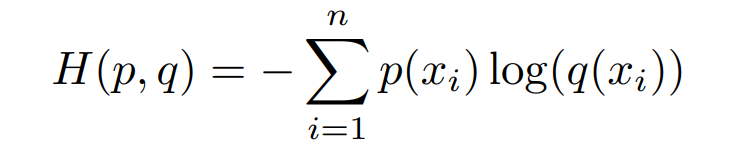
Binary cross entrophy

Now we can define our cost function using binary cross entrophy, which measures the error that the hypothesis made and to minimize it. The binary cross entrophy is defined as:

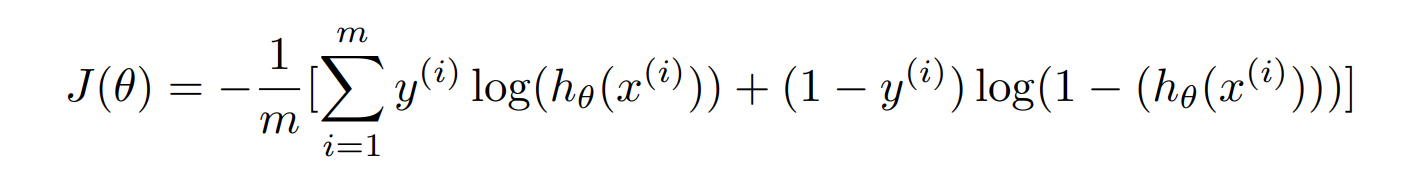
And we can also use gradient descent to minimize the logistic regression cost function:

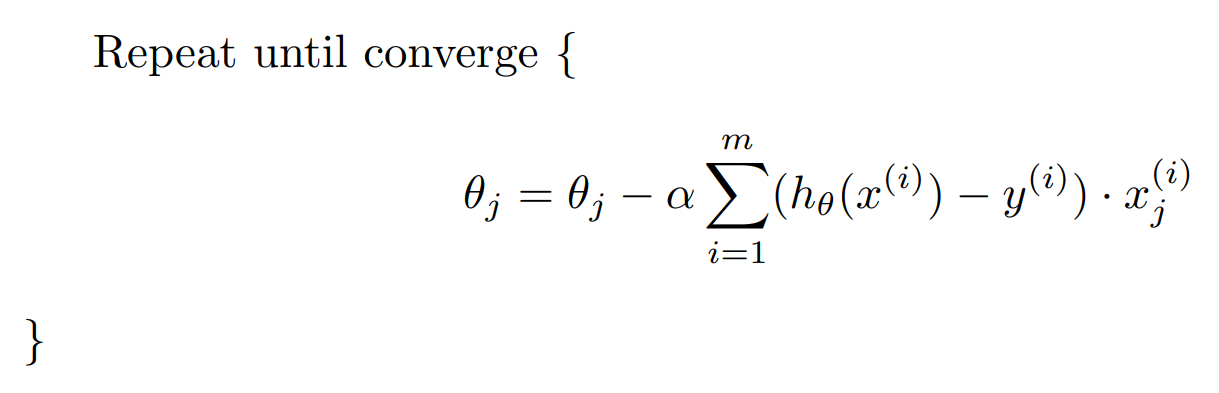
Advanced Optimization

Previously we focused on how to optimize gradient descent. Now let’s focus on advanced concepts for minimizing the cost function for logistic regression.

Instead of gradient descent to minimize the cost function, we could use these more optimized but complicated algorithms:

1. Conjugate gradient
2. BFGS (Broyden-Fletcher-Goldfarb-Shanno)
3. L-BFGS (Limited memory - BFGS)

Advantages of using these optimized algorithms:

1. No need to manually adjust learning rate.
2. Faster than gradient descent.
3. Can be used successfully without knowing its details.

Disadvantages of using these optimized algorithms:

1. Could make debugging more difficult.
2. Should not be implemented themselves.
3. Different libraries may use different implementations - may hit performance.

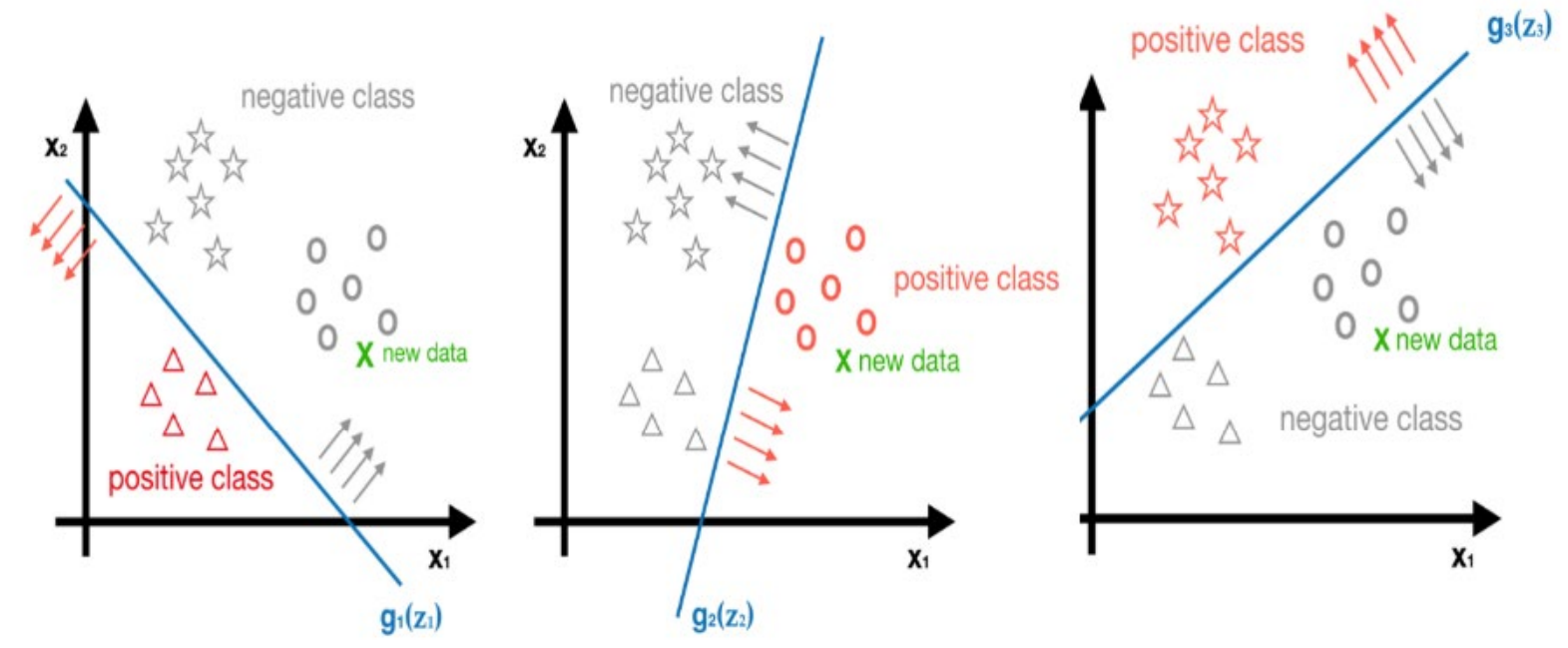
Multi-class classification

Here, we introduce a common method based on logistic regression, called one-vs-all or one-vs-rest.

The core idea of one-vs-all method is to classify the dataset into positive class and negative class (i.e. goal class and the other classes) at each time, and then to get the probability of being the positive class. After calculating the probabilities of being all positive classes, we choose the maximum one as the predictor’s result.